Scientific/Signal API
Class: LinearFilter
New in SDK 3.0
A LinearFilter represents any Finite Impulse Response (FIR) or Infinite
Impulse Response (IIR) linear filter. It provides a convenient mechanism
for keeping track of the entire configuration and state for such a
filter, but is just a convenience: It contains no hidden state, and could
be reconstructed every update from its constituent fields, if desired.
The filter is represented in transfer function form, as arrays of
numerator and denominator coefficients. The filter is realized in direct
form II, requiring only a single array of delay elements with length
max(b.length, a.length) - 1.
For the purposes of local design and debugging, the following should be equivalent:
JavaScript
import { LinearFilter } from "scientific/signal";
var filt = new LinearFilter(b, a, zi);
var y = filt.update(x);
var zf = filt.z;
Python
y, zf = scipy.signal.lfilter(b, a, x, zi)
Example
As a simple example, a butterworth bandpass filter can be constructed as follows:
import { LinearFilter } from "scientific/signal";
Generate some sample data
Typically this would come from an accelerometer, gyro, or other sensor.
const numSamples = 4096;
const sampleFreq = 44100;
const X = new Float32Array(numSamples);
for (let i = 0; i < X.length; i++) {
const t = i / sampleFreq;
// Form a signal containing a 50 Hz sinusoid of amplitude 0.7
var S = 0.7 * Math.sin(2 * Math.PI * 50 * t);
// ...and a 120 Hz sinusoid of amplitude 1.
S += Math.sin(2 * Math.PI * 120 * t);
// Corrupt the signal with zero-mean white noise with a variance of 4.
X[i] = S + 2 * Math.random()
}
Construct a filter
Typically this would be done at application startup, and the same filter(s) reused for the duration of application execution.
const filter50hz = new LinearFilter(
new Float32Array([2.88394643e-09, 0.0, -8.65183928e-09, 0.0, 8.65183928e-09, 0.0, -2.88394643e-09]),
new Float32Array([1., -5.99415495, 14.97093756, -19.94220015, 14.94252458, -5.97142422, 0.99431717]));
b and a filter coefficients were calculated using scipy.signal
Python
nyquist = 0.5 * sampleFreq
b, a = scipy.signal.butter(3, [40 / nyquist, 60 / nyquist], btype='band')
Update the filter
Typically this would be done each time new sensor samples come in:
const y = filter50hz.update(X);
y contains the frequency components of X between 40hz and 60hz, with
the 120Hz signal and noise filtered out. 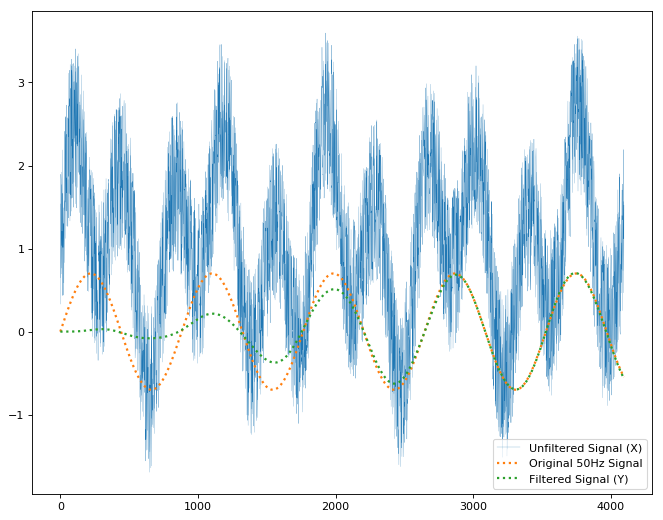
See the example Scientific app on Github
Properties
readonly a
Float32Array
a represents a copy of the coefficients of the polynomial
describing the denominator in the form:
a[0] + a[1]z^-1 + ... + a[N]z^-N
If a[0] is not 1, both a and b are normalized by a[0].
readonly b
Float32Array
b represents a copy of the coefficients of the polynomial
describing the numerator in the form:
b[0] + b[1]z^-1 + ... + b[M]z^-M
readonly z
Float32Array
z represents a copy of the internal state of the filter delay
elements. If not provided, defaults to an array of zeros.
Methods
update()
update(x: Float32Array)
Returns: Float32Array
update runs each of x's data points through the filter, updating
the internal state z at each iteration, and returning the filter
output as a Float32Array.





